Identification of lasso topology relies on detection of piercings through a minimal surface spanned on a covalent loop. Detection of piercings for each loop consists of four steps which are described in detail in [1-2] and in extensive supplement to [2]:
The covalent loops considered are build on the backbone of the chain and are closed by a bridge joining side groups (more about possible bridges in section "Determination of bridge type"). As for small loops the probability of threading is negligible, we impose the condition, that the loop has to have length of at least 5 residues. However, the server option allows user to choose any loop size larger than or equal to 3 residues.
Furthermore, we check the geometry of the loop. To that end we impose several conditions to obtain robust results:
The first condition follows from the fact, that the Cα-Cα distance spans a narrow range centered at 3.8 Å. Moreover, the range was extended to lower distances, as in the case of a gapped chain, the line fragment which models the gap can introduce shorter than native distances between consecutive Cα atoms.
The second condition follows from the distribution of Cα-Cα distances of bridge building residues (Fig. 1). In the case of cysteines, the shortest non-artificial distance found by us was equal to 3.3 Å. On the other hand, the maximal distance found by us was less then 10 Å.
Furthermore, in our analysis we check the input file. In particular we look for atoms/residues with the same index and we check the order of the atoms, as one with a lower index should precede one that is higher. This eliminates singular cases, where the coordinates of the loop forming atoms are given in the wrong way.
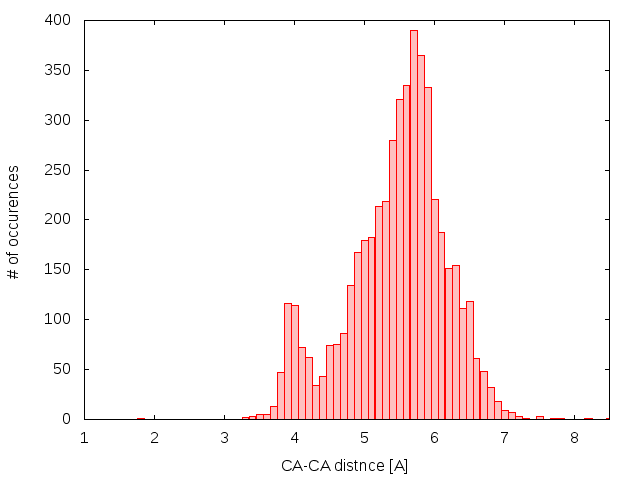
Fig.1 Histogram of Cα-Cα distances in cysteine bridges based on set of all cysteine bridges in nonredundant set of proteins (5014 bridges).
After filtering the appropriate covalent loop, the next step in lasso detection is spanning the surface on the closed loop. There is however an infinite number of surfaces which can be spanned on the given loop. This would potentially hinder our analysis, as the piercing pattern would depend on the surface definition. Therefore, to achieve stability of our results we model the minimal surface on a given closed loop. Minimal surfaces are the surfaces of soap bubbles spanned on a closed loop. They are the (local) energetic minimas (minimas of Dirichlet energy functional), hence they are stable solutions for the problem of finding the surface spanned on a given loop. We should however point out, that the locality of the energetic minimum can introduce some ambiguity, as there could be potentially a surface with lower global area (and therefore the surface energy of a soap bubble), while we find only the local minimum. Therefore it is possible, that the result would still depend on the choice of one out of a few minimal surfaces. However, throughout all our analysis, we did not encounter any such ambiguity.
Spanning of minimal surface on a given covalent loop requires an efficient algorithm of its construction. First of all, in most cases we are able only to approximate the minimal surface by its triangulation, i.e. to create the mesh of triangles, whose mean "distance" from actual minimal surface is small enough (Fig. 2).
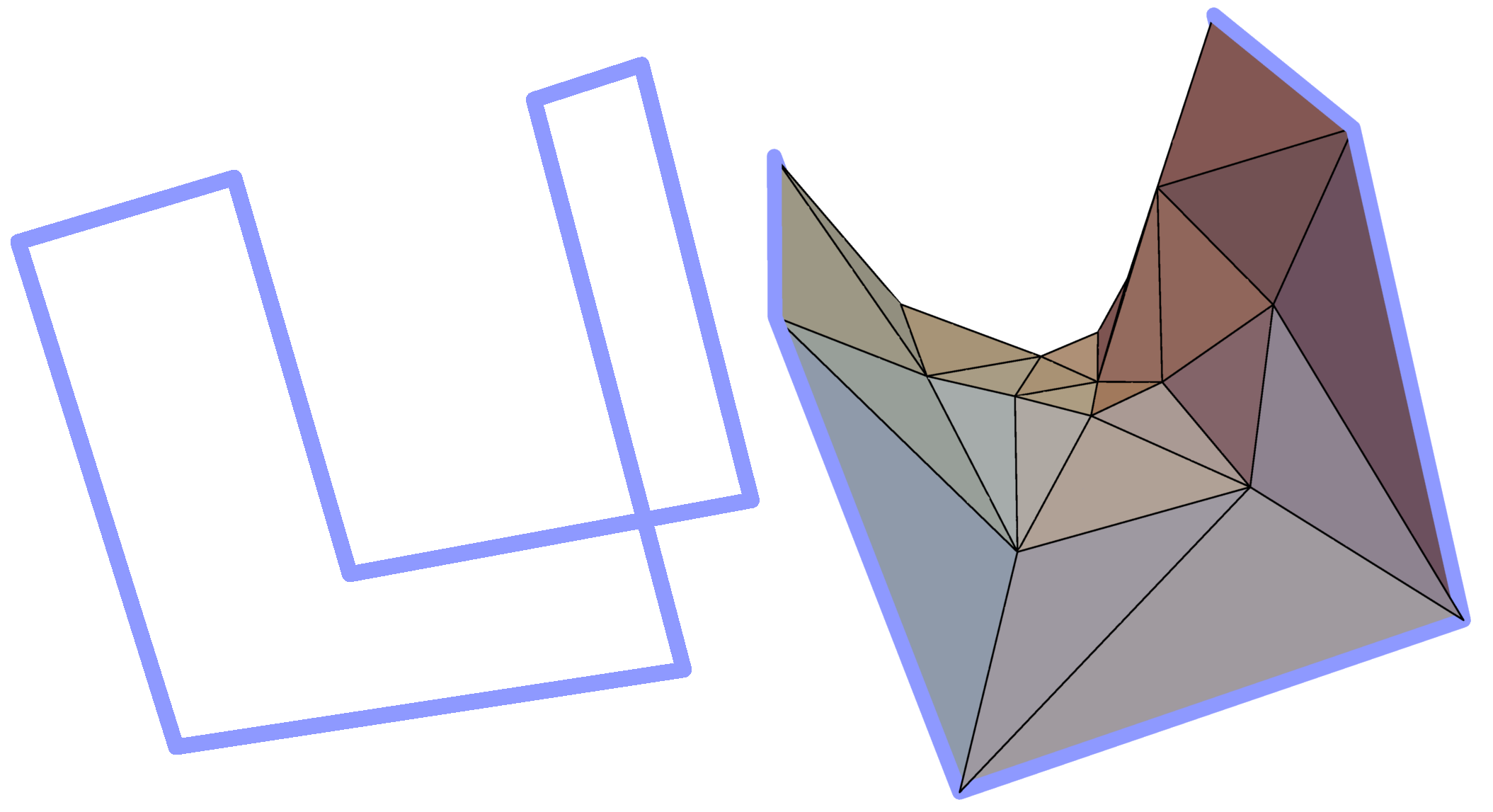
Fig. 2 Example simple polygon in three-dimensional space (left panel) and a triangulated minimal surface spanned on it (right panel).
There are several algorithms, used in particular in computer graphics, that determine such triangulations. In our work we implemented a slightly modified version of an algorithm discussed in [1]. The initial data for this algorithm consists of coordinates of n vertices in the covalent loop and the number of triangles in the triangulation that we are going to construct. This number one to adjust the level of details of the resulting mesh - the larger the number, the surface is approximated more accurately. Once some initial mesh has been specified, we iteratively adjust it by performing three operations that minimize the (local) area and the Dirichlet energy: Area Minimizing, Laplacian Fairing and Edge Swapping. We quit the iteration if the modification of a triangulation in a given step does not change the surface area sufficiently. A detailed description of the algorithm used is contained in the suplement to [2].
Moreover, as the protein chain is oriented from N- to C-terminus, our analysis enables us to unequivocally orient the surface (the method introduced in [3]). The orientation is spread across all the triangulated surface starting from the triangle closest to the bridge. To orient this triangle, first we form two imaginary vectors, beginning in the “opening” cysteine. One points towards the “closing” cysteine, the second one towards the next atom in the chain (according to its index). The vector product of these two (in this exact order) gives rise to a vector, which we arbitrarily call positively directed (Fig. 3).
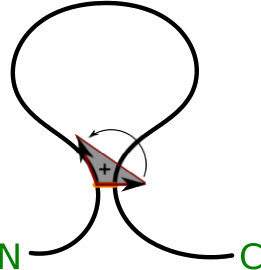
Fig. 3 Schematic depiction of definition of the orientation of the surface, N and C corresponds respectively to the N- and C-terminus (based on [3]).
Once the triangulation of the minimal surface is determined, we can verify which segments of the lasso protein tail (or tails) pierce the surface. This is done by checking, if the vector joining two consecutive Cα atoms of the tail pierces any of the triangles forming the surface. If it does so, the index of the atom from the end of the piercing vector is reported along with the direction of crossing i.e. the reverted sign of scalar product between the "positive direction" vector of the surface and the piercing vector (Fig. 4). The direction of piercing is determinable only if the surface is orientable which in our work was always the case. In the depiction of the triangluated surface we denote the direction of piercing by drawing pierced triangles in different colors (e.g. in Fig. 5 blue and green triangles are pierced from opposite directions), and label the segments of a tail that pierce the surface with plus or minus signs respectively (e.g. tail segments denoted -10 and +289 in Fig. 5 pierce the surface from opposite directions).
Note that some proteins have a complicated backbone configuration, giving rise to complicated, self intersecting surfaces as discussed in detail in the supplement of [2]. In such cases it is convenient to present the triangulated surface as a planar barycentric graph, in which each vertex of a triangulation is an average of the vertices it is connected to. By a theorem by Tutte, such representation can be uniquely determined purely from the connectivity structure of a triangular surface. We use a well known algorithm by Tutte [4] to determine such barycentric representation. However, the original algorithm forces the triangles to be most densely packed in the vicinity of the limiting circle. Therefore, we add a hyperbolic transformation shifting the vertices of triangles towards the center, which improve the presentation. As an example, such planar barycentric graph for triangulated minimal surface spanned on a covalent loop in the Glutamate receptor with pdb code 3OM0, is shown in Fig. 5.
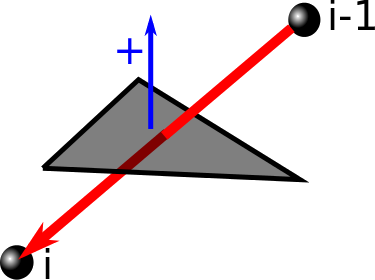
Fig. 4 Schematic representation of method to detect, which segment of the protein tail pierces the minimal surface. Here the surface piercing is represented just by one triangle.
Data included in the LassoProt rely on the method described above. However, to ensure transparency of the results we are providing all details about self intersecting surfaces and detected crossing (see also Reduction of artificial crossings below) via files to be downloaded (see Data presentation and Trajectory analysis). We would like to stress that the criterions suitable for proteins, established in [1], could not be optimal for other bio-polymers. Therefore we provide users the option to formulate own conditions to detect crossing via Advanced options in the server (see Single structure analysis).
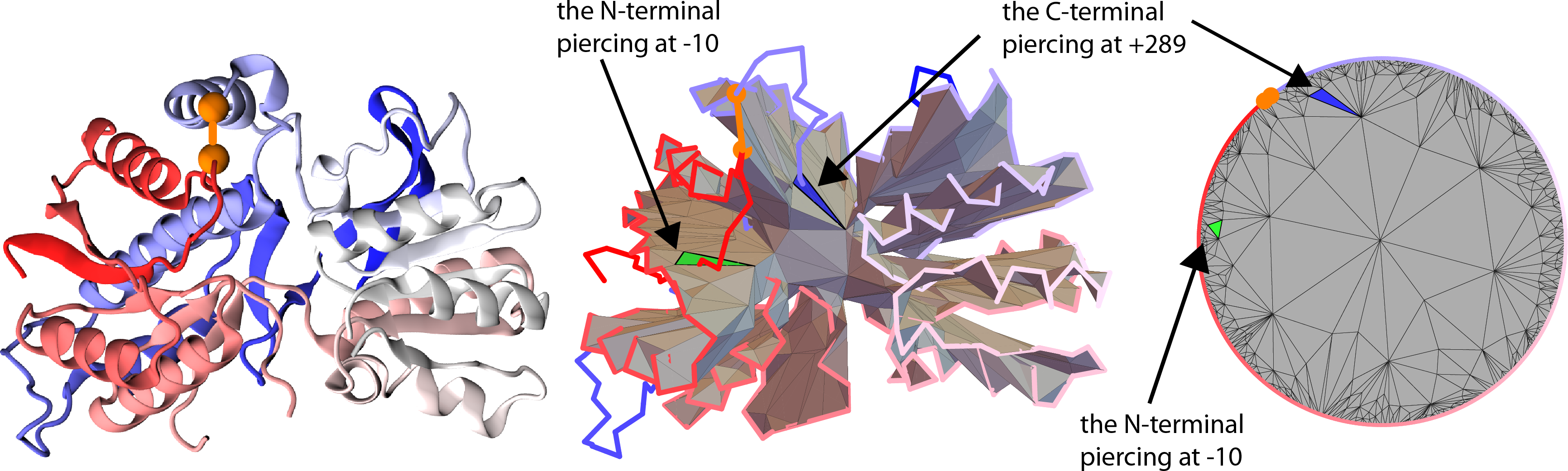
Fig. 5 Glutamate receptor with pdb code 3OM0 in its cartoon representation, along with the minimal surface prescribed for it and a barycentric graph. In the barycentric graph two pierced triangles (blue and green one) are indicating the L2 topology of the loop.
In our analysis we try not to include proteins which lasso structure could be changed by thermal fluctuations of the chain. Therefore, we impose a condition that there must be at least 10 amino acids separation between consecutive piercings (from opposite directions), i.e. a piece of a tail piercing a surface must be sufficiently “deep”. There is one exception to this rule. Observe in Fig. 6 that one may find a complex protein structure, where a minimal surface spanned on a covalent loop, has two distinct pieces located close to each other. In such a case a tail may pierce both pieces of the surface and have less than 10 amino acids between these two crossings, but nonetheless we include such structures in our analysis. To detect such configurations automatically, we compute (using Dijkstra algorithm) the shortest distance (along segments of the triangulation of the minimal surface) between two triangles that are pierced by a tail. If this distance is long enough (larger than 10 segments of the mesh) we include such a structure in our classification.
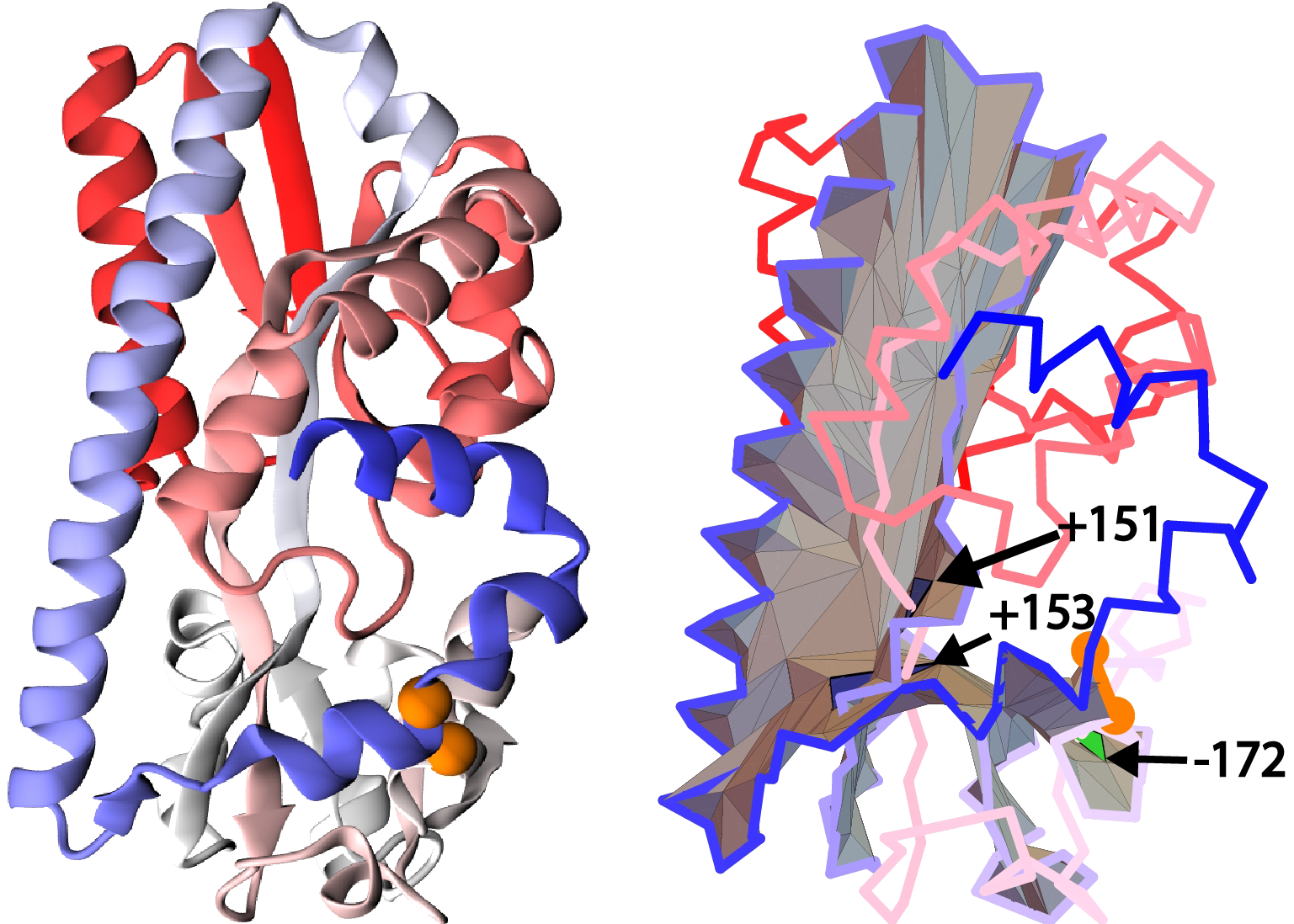
Fig. 6 Example of a unique configuration when a segment of less than 10 residues between consecutive crossings is accepted via our method based on protein with pdb code 4P1E (cartoon representation of structure - left panel, the surface spanned in the right panel). Figures show a tail segment shorter than 10 amino acids piercing two spatially separated parts of the self-intersecting surface.
We also demand the segment between the cysteine bridge and the first piercing to include at least 3 amino acids (see Fig. 7), as the crossings located in close vicinity of the loop can be the effect of random movement of the protein chain. Furthermore, we require the crossing to be located at least 3 residues from the closest terminus, once again, for the crossing to be sufficiently “deep”.
The piercings, which are considered to be artificial are reduced, and are not shown in the default crossing list, nor determine the covalent loop class. However, in order to maintain the transparency of the process, the reduced crossings can be vied for all the closed loops (more about protein presentation in Single protein chain data presentation section). Moreover, via the Advanced options users can create their own conditions to distinguish between artificial and correct piercings.
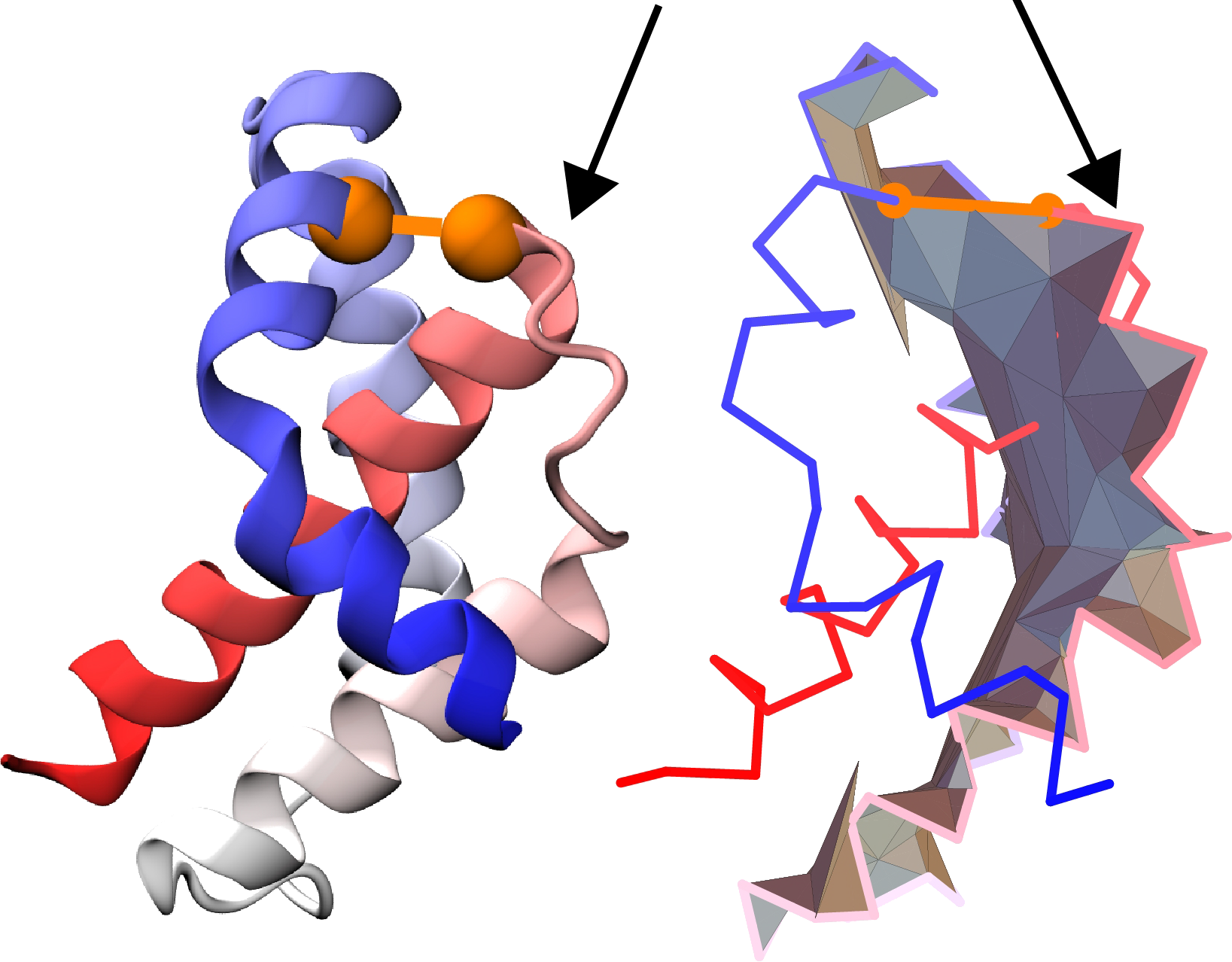
Fig. 7 Example of artificial piercings - the piercing (indicated by an arrow) is located too close to the bridge, based on [1] (cartoon presentation - left panel, triangulated surface - right panel).
